目镜
目镜eyepiece,用来观察前方光学系统所成图像的目视光学器件,是望远镜、显微镜等目视光学仪器的组成部分。为消像差,目镜通常由若干个透镜组合而成,具有较大的视场和视角放大率。
含义[编辑 | 编辑源代码]
目镜也是显微镜的主要组成部分,它的主要作用是将由物镜放大所得的实像再次放大,从而在明视距离处形成一个清晰的虚像;因此它的质量将最后影响到物像的质量。在显微照相时,在毛玻璃处形成的是实像。某些目镜(如补偿目镜)除了有放大作用外,还能将物镜造像过程中产生的
残余像差予以校正。目镜的构造比物镜简单得多。因为通过目镜的光束接近平行状态,所以球面像差及纵向(轴向)色差不严重。设计时只考虑横向色差(放大色差)。目镜由两部组成,位于上端的透镜称目透镜,起放大作用;下端透镜称会聚透镜或场透镜,使映像亮度均匀。在上下透镜的中间或下透镜下端,设有一光栏,测微计、十字玻璃、指针等附件均安装于此。目镜的孔径角很小,故其本身的分辨率甚低,但对物镜的初步映像进行放大已经足够。常用的目镜放大倍数有:8×、10×、12.5×、16×等多种。
目镜类型(按构造形式分)[编辑 | 编辑源代码]
1.福根目镜:目镜可分正型目镜系和负型目镜系两类。正型目镜的主焦点在场透镜以外,虽然由二个或两个以上的透镜组合而成,但整个光学系统可视为单一的凸透镜,故在适当情况下可单独作为放大镜使用。负型目镜的主焦点是在场透镜以内,即在场透镜与目透镜两个透镜之间,显然不能单独作为放大镜使用。最简单类型的目镜的焦点在两透镜之间,属于“负透镜”。福根目镜是负型目镜系中最简单的一种。它由二块分的没有经过色差校正的平凸透镜组成,接近人眼的一块称为目透镜,它起放大作用。另一块称为场透镜,它起使映像高度均匀的作用。在二块间装有一光栏,位于目透镜的前焦点
处。福根目镜未进行像差校正,或仅作部分球差校正,仍有一定程度的像差和畸变。其放大倍数一般不超过15倍,适应于配合中、低倍物镜,用作观察或摄影。
2.雷斯登目镜:由两个平凸透镜组成,其主焦点在下透镜(场透镜)之外,故称正透镜。雷斯登目镜对像场弯曲和畸变有良好的校正,球差也较小,但放大色差比福根目镜差。它除用于观察和摄影外,也可用于放大。
3.补偿目镜:垂轴色差为1.5%~2%的平场消色差物镜、平场半复消色差物镜、平场复消色差物镜等,都属于垂轴色差校正不足的物镜。这些物镜需要与垂轴色差校正过头的目镜配合使用,故称这种目镜为补偿目镜。补偿目镜具有过度的校正放大色差的特性,以补偿复消色差、半复消色差物镜的残余色差。由于补偿目镜具有一定量的垂轴色差及其放大倍数较高(高达30倍),不宜与普通消色差物镜配合使用,宜与复消色差物镜或半复消色差物镜配合使用,以抵消这些物镜的残余色象差。不可与消色差物镜配用,因为有“过正”产生,会使映像产生负向色差。
4.测微目镜:在目镜中加入一片有刻度的玻璃薄片,用来定量测量,或进行显微压痕长度的测量。根据测量目的可将刻度设计在直线、十字交叉线、方格网、同心圆或其他几何图形上。
5.摄影目镜: 此目镜专门用于摄影或近距离投影,不能用作显微观察或单独放大。其像差校正与补偿目镜基本相同,宜与平面复消色差物镜或半复消色差物镜配用,使在规定放大倍数下具有足够平坦的映像。
6.广角目镜:一般目镜视场角度在30°左右。广角目镜是指视场角在50°以上,放大倍数在12.5倍以上的平场目镜,和视场角在40°以上,放大倍数在10倍以下的平场目镜。
目镜特征[编辑 | 编辑源代码]
1.目镜的标记 目镜上刻有如下标记:目镜类别、放大率。例如10×平场目镜刻有p10×;p即表示平场目镜,10×为放大率,一般惠更斯目镜不刻标记。
2.目镜的放大倍数 目镜放大倍数是有规定的。目镜的作用是把物镜放大的实像(中间像)再放大一遍,并把物像映入观察者的眼中,实质上目镜就是一个放大镜。已知显微镜的分辨率能力是由物镜的数值孔径所决定的,而目镜只是起放大作用。因此,对于物镜不能分辨出的结构,目镜放
的再大,也仍然不能分辨出。
由于不同系列目镜光学设计不同,所以不能混用。
观测用的目镜依其焦距来区分其放大倍率,目镜的焦距愈长,数字愈多其放大倍率愈小,视野也就愈大。
一般而言40毫米以上,称之为低倍目镜,适合观测星云、星团、彗星等微光、暗淡天体。
25毫米—12毫米,称之为中倍目镜,适合观测月面、行星、双星及明亮星云内部。
12毫米—4毫米称之为高倍目镜,适合观测月面细部坑洞、行星表面、双星等。
对于各种不同的天体,要依不同对象选择不同焦距的目镜,一般市售望远镜均附有二三个目镜,分为中、高、低(如12毫米,6毫米,25毫米)或是中、高倍(如18毫米,6毫米)配备。建议倘若有机会应另外添购40毫米长焦专用低倍目镜,它们在观看星云、星团时效果特别地好。
值得注意的一点是,普通目镜的规格是24.5毫米,另外还有3种”大头”目镜的规格是31.7毫米、36.4毫米、50.8毫米,直径变大使目镜玻璃也变大,观看起来就像看大屏幕的电视一样。
决定功能的基本性质[编辑 | 编辑源代码]
目镜的一些性质对光学产品的功能非常重要,需要比较以决定最适合需求的目镜。
入射光瞳的距离设计[编辑 | 编辑源代码]
目镜的入射光瞳永远不变的被设计在目镜的光学系统之外,它们必须被设计在特定的距离上有优异的性能(即在这个距离上的变形极小)。在折射式的天文望远镜,入射瞳通常很靠近物镜的位置,与目镜通常有数英呎的距离;在显微镜,入射瞳通常紧靠着物镜的后焦平面,与目镜只有几英吋的距离。因此显微镜的目镜与望远镜的目镜性质不同,不是互换就能获得适当的表现。
元素和群[编辑 | 编辑源代码]
每一个独立镜片称为元素,通常是简单的透镜,可以组合成单镜、胶合的双镜或是三合镜。当这些元素被两个或三个黏合在一起时,这种组合就成为群。
第一个目镜只是单片的透镜元素,得到的影像有高度的变形。二或三个元素的设计发明之后,由于改进了影像的品质,很快就成了标准的设计。今天,工程师在计算机协助规划下的设计,以七或八个元素提供了绝佳的影像。
内部反射和散射[编辑 | 编辑源代码]
内部反射有时也称为散射,导致穿过目镜的光线不仅分散还降低了目镜产生影像的对比。当影像的效果很差时就会出现"鬼影",称为幻像。多年以来,设计时玻璃与玻璃之间制造很小的空气隙,就能有效的改善这个问题。
对薄透镜可以采用在元素表面镀膜的方法来解决这个问题。这一层厚度只有一或两个波长的膜,可以改变通过元素的光线折射来减少反射和散射。有些镀膜可经由全反射的过程吸收这些光线以低浅角度射入的光线,使它们不会穿过透镜。
侧向色差[编辑 | 编辑源代码]
目镜
色差的产生是因为不同的颜色(波长)由一种介质到另一种介质时,有不同的折射率。对目镜而言,色差来自穿越空气和玻璃之间的界面。蓝光和红光在经过目径的元素之后不能距焦在同一个焦点上,这种现象对点光源 的结果是可能产生一个围绕着焦点的模糊色环,通常的结果是造成影像模糊不清。
有几种方法可以减缓这个问题,一种是利用薄膜来改正目镜的元素。较为传统的方法则是利用多个不同玻璃和曲度的元素来消减变形。
纵向色差在光学望远镜中,因为焦距很长而成为很显著的效应;显微镜,因为一般的焦距都很短,就不受这种效应的影响。
通常,目镜在改善色差时,这两种都需要做修正。
焦长(焦距)[编辑 | 编辑源代码]
焦长是平行的光经过目镜后汇距的点与目镜主平面的距离。在使用时,目镜焦长和物镜焦长的结合,确定了附属的放大倍率。当单独提到目镜时,他的单位通常是毫米(mm);而当在一架可以更换目镜的仪器上使用时,有些用户喜欢使用经过目镜后所能得到的放大倍数做为单位。
对望远镜,一些特殊的目镜可以产生不同的角放大率,并且望远镜和显微镜的组合倍率可以用下面的惯例式来计算:MA是要计算的角放大倍率,fO是望远镜物镜的焦长,fE是目镜的焦长,要用同样的测量单位来表示。fT对一个复合式显微镜的惯用式是距离最接近的明视距离(通常是250mm),DEO是物镜的后焦面和目镜的后焦面(称为筒长)的距离,在现代的仪器上这个距离通长是160mm O是物镜的焦长,FE是目镜的焦长。因此,要提高放大倍率,可以将目镜的焦长减短,或是将仪器本身的焦长
加长。例如,焦长25mm的目镜用在焦长1200mm的望远镜上,放大倍率是48倍;焦长4mm的目镜用在相同的望远镜上,放大倍率是300倍。
业余天文学家使用的望远镜的目镜倾向于将焦长标示出来。在天文学,焦长的表示单位通常是毫米(mm),范围则在3至50毫米间。实际的放大倍率则依使用的望远镜的焦长来决定。
但是当描述观测现象时,天文学家对于目镜的标示,却又惯用放大倍率,而不是标示目镜的焦长。在观测报告上使用放大倍率是比较方便的,因为它更直接的提示了观测者实际上看到的是什么的看法。由于放大倍率是依赖所使用的望远镜决定,因此单独只提放大倍率对望远镜的目镜是毫无意义的。
依据协议,显微镜的目镜通常标示具体的倍率来取代焦长。显微镜的倍率 PE和物镜的倍率PO因而对一个复合式的显微镜前端角放大率的表示是:
倍率的定义是依据仪器对任易分离角度在目镜和物镜之间被放大的能力。不同于历史上对显微镜目镜的分析,是依据目镜对角度的放大倍率,和物镜原本的放大能力。这对光学设计师是很方便,但从显微镜学实用的观点上看却缺乏便利性,因此便被摒弃了。 一般目镜的放大倍率是8X、10X、15X、和20X。这些倍数是与正常人的能看清楚的最短明视距离,D250mm,比较得到的,所以目镜的焦距可以用250mm除以放大倍率而计算出来。虽然被接受的标准距离是250mm,但现在的显微镜会设计成只有160mm的焦距,使得仪器变得非常的紧凑。现在的仪器也许还会被设计成管子实际上是无限长的(在镜筒内使用一个辅助透镜)。 显微镜影像整体的角放大率是目镜放大率与物镜放大率的乘积。例如,10X的目镜与40X的物镜组合就会得到400X的放大倍数。
焦平面的位置[编辑 | 编辑源代码]
有一些目镜,像是冉斯登目镜 ,焦平面的位置在目镜之外的场透镜前方,因此很适宜做为标线或测微表等十字线安置的位置。在惠更斯目镜,焦平面的位置在眼睛和在目镜内的场透镜之间,是不容易接近的位置。
视野[编辑 | 编辑源代码]
视野,经常会使用缩写FOV,描述的是经由目镜能看见的目标 (从观测者所在地测量得到的角度) 。目镜的视野范围会根据各自所结合的望远镜或显微镜的放大率而有所变化,也和目镜本身的性质有关。目镜由他们的视野阑做区分,这是进入目镜的光线抵达场透镜前所经过的最狭窄孔径。
由于这些可变的因素,"视野"这个名词通常有两种意义,并且总是只表示其中之一。
实视野是使用某一架望远镜时,由于具体的放大效果,通过目镜能看见的真实天空的角度大小,它的范围通常在0.1度至2度间。视视野是被测量的目镜所有的一个恒定值,范围从35度至80度以上。它本身,明显的是一个抽象的数值,但是可以经由望远镜与目镜结合所得到的的放大率测量出实视野。目镜的视视野通常都会作为目镜的特性标示出来,为用户提供一个便的方法,计算在自己的望远镜上使用时的实视野。目镜的使用者通常都需要计算实视野,因为这表示出目镜与望远镜结合时,实际上能看见的天空大小。计算实视野最方便的方法取决于是否知道视视野。 如果已经知道视视野,实视野可以经由下面的近似公式计算:
FOVC是实视野,计量的单位是以FOVP时所提供的角度单位来测量。.FOVP 是视视野。mag是放大倍数。fT是望远镜的焦长。 E是目镜的焦长,用与fT相同的量度单位来标示。望远镜物镜的焦长是物镜的口径乘上焦比的值,他代表镜子或透镜将光线聚集在一个点上的距离。
这种形式的精确度可以在4%以内,或视视野达到40°都是良好的,而在60° 时的误差为10%。 如果不知道视视野,实视野可以使用下面的方法来概估: FOVC 是实视野,以度为计算单位。d是目镜视野阑的直径,单位为mm。fT式望远镜的焦距,单位为mm。第二个式比第一个来得精确,但是多数厂家通常都不会告知视野阑的大小。如果视场不是平坦的,或是对设计的角度大于60°的超广角目镜,第一个式就会不准确。
筒径[编辑 | 编辑源代码]
目镜
最小的标准筒径是0.965 英吋 (24.5mm),但几乎已经被摒弃了。仍然使用这种筒径的望远镜不是玩具店内的商品,就是通常只在商城 (大卖场) 内仍然充斥的品质较差的望远镜。许多在这种望远镜上的目镜都是塑胶制造的,有些甚至连透镜都是塑胶的。高品质的望远镜早已不再种尺寸的目镜了。大部分的目镜筒径都是1¼ 英吋 (31.75mm),这种筒径的目镜在实用上的焦距上限大约是32mm。焦
距更长的目镜,焦距比32mm更长的目镜,筒径的边缘限制了视视野的大小不能超过50°,而多数的业余者认为这是可以接受的最小视野。这种筒径的螺旋可以置入30mm的滤镜。
2 英吋 (50.8 mm) 筒径的目镜经常被使用。2英吋目镜的焦距极限大约在50mm,大于2英吋 (50.8 mm) 的筒径主要在协助延伸目镜焦距的极限。这种目镜的价值通常都很昂贵,并且可能重得足以倾覆望远镜。这种目镜的螺旋适用48mm的滤镜 (或是49mm的)。显微镜的目镜使用mm为单位,标准筒径为23.5mm和30mm,都比望远镜的筒径小一些。
适眼距[编辑 | 编辑源代码]
眼睛需要在目镜后方的一段距离内观看经过目镜形成的影像,这段适当的距离称为适眼距。有着较大的适眼距,意味着目镜的品质越佳,也越容易观看到影像。但是如果适眼距太大,要让眼睛长期处在正确的位置上,它会造成眼睛的不舒适。基于这个原因,有些有着长适眼距的目镜,在目镜透镜的后方有眼罩
杯的设计,可以帮助观测者能长时间的在正确的距离上观测目标。出射瞳的大小应该与拉姆斯登盘的大小相符。在天文望远镜的情况下,入射光瞳的影像对应于物镜的大小。
适眼距的典型范围在2mm至20mm之间,依据目镜的构造来决定。长焦距的目镜通常都有较宽裕的适眼距,但短焦距目镜的适眼距就有问题了。直到最近,这仍然是相当普遍与共通的,短焦点目镜的适眼距就较短。好的设计指南建议适眼距至少要有5-6mm,以避免睫毛造成的不舒适。现代的设计可以增加许多透镜元件,不仅在这方面获得改善,还可以在高倍率的观测上变得更加舒适。特别是对于带眼镜的观测者,他们至少需要20mm的距离才能容纳德下它们的眼镜。
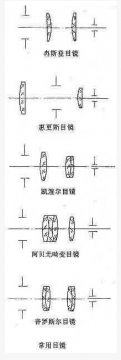
天文望远镜的目镜种类与结构[编辑 | 编辑源代码]
惠更斯目镜(H式或HW式)[编辑 | 编辑源代码]
荷兰科学家惠更斯于1703年设计,有两片平凸透镜组成,前面为场镜,后面为接目镜,他们的凸面都朝向物镜一端,场镜的焦距一般是接目镜的2-3倍,镜片间距是它们焦距之和的一半。惠更斯目镜视场约为25-40度。过去,惠更斯目镜是小型折射镜的首选,但随着望远镜光力的增大,其视场小,反差低,色差,球差场曲明显的缺点逐渐暴露出来,所以目前这种结构一般为显微镜的目镜采用。
冉斯登目镜(R式或SR式)[编辑 | 编辑源代码]
于1783年设计成功,也是两片两组结构,由凸面相对,焦距相同的两个平凸透镜组成。间距为两者焦距和的2/3-3/4,其色差略大,场曲显著减小,视场约为30-45度,目前已很少采用。
凯尔纳目镜(K式)[编辑 | 编辑源代码]
是在冉斯登目镜的基础上发展而来,出现于1849年,主要改进是将单片的接目镜改为双胶合消色差透镜,大大改善了对色差和边缘像质的改善,视场达到40-50度,低倍时有
着舒适的出瞳距离,所以目前在一些中低倍望远镜中广泛应用,但是在高倍时表现欠佳。另外,凯尔纳目镜的场镜靠近焦平面,这样场镜上的灰尘便容易成像,影响观测,所以要特别注意清洁。美国一家司在凯尔纳目镜的基础上进一步改进,研制出了RKE目镜,其边缘像质要好于经典结构。
阿贝无畸变目镜(OR式)[编辑 | 编辑源代码]
1880年由德国蔡司公司创始人之一的阿贝设计,为四片两组结构,其中场镜为三胶合透镜,接目镜为平凸透镜,该目镜成功的控制了色差和球差,并把鬼像和场曲降低到难以察觉的程度,它还具有40-50度的平坦视场和足够的出瞳距离,在各倍率都有良好表现,一直被广泛采用。
爱勒弗广角目镜[编辑 | 编辑源代码]
1917年研制成功,是专门为需要大视场的军用望远镜设计,是其后所有广角目镜的鼻祖,结构为5片三组,视场高达60-75度。非常适合观测深空天体,由于边缘存在像散,所以不太适合高倍设计,其在低倍时的表现是非常出色的。
普罗素目镜(PL式)[编辑 | 编辑源代码]
又称为对称目镜。由完全相同的两组双胶合消色差透镜组成,其参数表现与OL目镜相当,但具有更大的出瞳距离和视场,造价更低,而且适用于所有的放大倍率, 是目前应用最为广泛的目镜,曾派生出多种改进型。
Nagler目镜[编辑 | 编辑源代码]
一种于1979年由美国人设计的高档目镜,有着82度的惊人视场,优质的边缘像质和舒适的出瞳距离,以及复杂的结构和高昂的价格,和超过一公斤的重量。