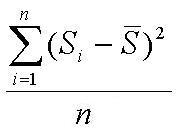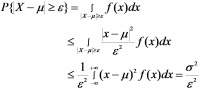方差
在概率论和数理统计中,方差(英文Variance)用来度量随机变量和其数学期望(即均值)之间的偏离程度。在许多实际问题中,研究随机变量和均值之间的偏离程度有着很重要的意义。如下面的例子:
已知某零件的真实长度为a,现用甲、乙两台仪器各测量10次,将测量结果X用坐标上的点表示如图:
甲仪器测量结果:
乙仪器测量结果:
两台仪器的测量结果的均值都是 a 。但是用上述结果评价一下两台仪器的优劣,很明显,我们会认为乙仪器的性能更好,因为乙仪器的测量结果集中在均值附近。
由此可见,研究随机变量与其均值的偏离程度是十分必要的.那么,用怎样的量去度量这个偏离程度呢?容易看到E(|X-E(X)|)能度量随机变量与其均值E(X)的偏离程度. 但由于上式带有绝对值,运算不方便,通常用量
E{[X-E(X)]^2} 这一数字特征就是方差。
方差的定义[编辑 | 编辑源代码]
设X是一个随机变量,若E{[X-E(X)]^2}存在,则称E{[X-E(X)]^2}为X的方差,记为D(X)或DX。
即D(X)=E{[X-E(X)]^2},而σ(X)=D(X)^0.5(与X有相同的量纲)称为标准差或均方差。即用来衡量一组数据的离散程度的统计量。
方差刻画了随机变量的取值对于其数学期望的离散程度。
若X的取值比较集中,则方差D(X)较小;
若X的取值比较分散,则方差D(X)较大。
因此,D(X)是刻画X取值分散程度的一个量,它是衡量X取值分散程度的一个尺度。
方差的计算[编辑 | 编辑源代码]
由定义知,方差是随机变量 X 的函数
g(X)=[X-E(X)]^2
的数学期望。即:
由方差的定义可以得到以下常用计算公式:
D(X)=E(X^2)-[E(X)]^2
证明:
D(X)=E[X-E(X)]^2
=E{X^2-2XE(X)+[E(X)]^2}
=E(X^2)-2[E(X)]^2+[E(X)]^2
=E(X^2)-[E(X)]^2
方差其实就是标准差的平方。
方差的几个重要性质[编辑 | 编辑源代码]
(1)设c是常数,则D(c)=0。
(2)设X是随机变量,c是常数,则有D(cX)=(c^2)D(X)。
(3)设 X 与 Y 是两个随机变量,则
D(X+Y)= D(X)+D(Y)+2E{[X-E(X)][Y-E(Y)]}
特别的,当X,Y是两个相互独立的随机变量,上式中右边第三项为0(常见协方差),
则D(X+Y)=D(X)+D(Y)。此性质可以推广到有限多个相互独立的随机变量之和的情况.
(4)D(X)=0的充分必要条件是X以概率为1取常数值c,即P{X=c}=1,其中E(X)=c。
常见随机变量的期望和方差[编辑 | 编辑源代码]
设随机变量X。
X服从(0—1)分布,则E(X)=p D(X)=p(1-p)
X服从泊松分布,即X~ π(λ),则 E(X)= λ,D(X)= λ
X服从均匀分布,即X~U(a,b),则E(X)=(a+b)/2, D(X)=(b-a)^2/12
X服从指数分布,即X~e(θ), E(X)= θ,D(X)= θ^2
X服从二项分布,即X~B(n,p),则E(x)=np, D(X)=np(1-p)
X 服从正态分布,即X~N(µ,σ2), 则E(x)=µ, D(X)=σ^2
若Xi~ N(µi,σi^2),i=1,2,…n, 且它们相互独立,则它们的线性组合C1X1+C2X2+…+CnXn(Ci是不全为0的常数)仍然服""从正态分布,且C1X1+C2X2+…+CnXn~N (∑Ciµi, ∑Ci^2σi^2)
统计学的应用[编辑 | 编辑源代码]
概念[编辑 | 编辑源代码]
样本中各数据与样本平均数的差的平方和的平均数叫做样本方差;样本方差的算术平方根叫做样本标准差。
样本方差和样本标准差都是衡量一个样本波动大小的量,样本方差或样本标准差越大,样本数据的波动就越大。
方差和标准差。方差和标准差是测算离散趋势最重要、最常用的指标。方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法。标准差为方差的平方根,用S表示。标准差相应的计算公式为
标准差与方差不同的是,标准差和变量的计算单位相同,比方差清楚,因此很多时候我们分析的时候更多的使用的是标准差。
高考实例[编辑 | 编辑源代码]
(甘肃省,2002年)某校初三年级甲、乙两班举行电脑汉字输入速度比赛,两个班参加比赛的学生每分钟输入汉字的个数,经统计和计算后结果如下表所示:
| 班级 | 参加人数 | 平均字数 | 中位数 | 方差 |
| 甲 | 55 | 135 | 149 | 191 |
| 乙 | 55 | 135 | 151 | 110 |
有一位同学根据上表得出如下结论:
①甲、乙两班学生的平均水平相同;
②乙班优秀的人数比甲班优秀的人数多(每分钟输入汉字达150个以上为优秀);
③甲班学生比赛成绩的波动比乙班学生比赛成绩的波动大.上述结论正确的是________(填序号).
解:填①、②、③,显然①、③是正确的是.对于第②个结论,因为甲的中位数为149,表明甲班优秀人数未过半,而乙的中位数为151,表明乙班优秀人数在半数以上,故乙班优秀的人数比甲班优秀人数多,∴ ②正确.
切比雪夫不等式[编辑 | 编辑源代码]
定理[编辑 | 编辑源代码]
设随机变量X就有数学期望E(X)=µ,方差D(X)=σ^2 ,则对于任意整数ε,有不等式
| 或 |
成立。
由切比雪夫不等式可以看出,若 ε 越小,则事件{|X-E(X)|< ε }的概率越大,即随机变量X 集中在期望附近的可能性越大.
就只连续性随机变量的情况来证明。
设X的概念密度为 f(x).
当方差已知时,切比雪夫不等式给出了r.v X与它的期望的偏差不小于3σ 的概率的估计式 .
如取ε =3σ
可见,对任给的分布,只要期望和方差D(X),则 r.v X取值偏离E(X)超过3σ 的概率小于0.111 .
应用实例[编辑 | 编辑源代码]
例9 已知正常男性成人血液中 ,每一毫升白细胞数平均是7300,均方差是700 . 利用切比雪夫不等式估计每毫升白细胞数在5200~9400之间的概率 .
解:设每毫升白细胞数为X
依题意,E(X)=7300,D(X)=7002
所求为 P(5200 ≤ X≤ 9400)
P(5200≤ X ≤ 9400)
= P(-2100 ≤X-E(X) ≤ 2100)
= P{ |X-E(X)| ≤ 2100}
由切比雪夫不等式,
即估计每毫升白细胞数在5200~9400之间的概率不小于8/9 .