球体
定义:空间中到定点的距离等于定长的所有点组成的图形叫做球,如图右图所示的图形为球体。
球面是一个连续曲面的立体图形,由球面围成的几何体称为球体。
球形的立体物
指球形的体育用品,球类运动,包括手球、篮球、足球、台球,排球、羽毛球、网球、高尔夫球、冰球、沙滩排球、棒球、垒球、藤球、毽球、乒乓球、台球、鞠蹴、板球、壁球、沙壶、冰壶、克郎球、橄榄球、曲棍球、水球、马球、保龄球、健身球、门球、弹球等。
球体的组成
球的表面是一个曲面,这个曲面就叫做球面。
球和圆类似,也有一个中心叫做球心。
星体,特指“地球”。
数学中的球体
球体基本概念
半圆以它的直径为旋转轴,旋转所成的曲面叫做球面。
球面所围成的几何体叫做球体,简称球。
半圆的圆心叫做球心。
连结球心和球面上任意一点的线段叫做球的半径。
连结球面上两点并且经过球心的线段叫做球的直径。
球体性质
用一个面去截一个球,截面是圆面。球的截面有以下性质:
1 球心和截面圆心的连线垂直于截面。
2 球心到截面的距离d与球的半径R及截面的半径r有下面的关系:r^2=R^2-d^2
球面被经过球心的平面截得的圆叫做大圆,被不经过球心的截面截得的圆叫做小圆。
在球面上,两点之间的最短连线的长度,就是经过这两点的大圆在这两点间的一段劣弧的长度,我们把这个弧长叫做两点的球面距离。
球体函数
半径为r的球的函数为:r^2=x^2+y^2+z^2
球体的计算公式
半径是R的球的体积 计算公式是:V=(4/3)πR^3(三分乘以π乘以半径的三次)
V=(1/6)πd^3 (六分乘以π乘以直径的三次)
半径是R的球的表面积 计算公式是:S=4πR^2(4倍的π乘以R的二次)
证明:
证:V球=4/3*pi*r^3
欲证V球=4/3pi*r^3,可证V半球=2/3pi*r^3
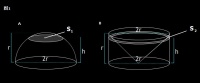
做一个半球h=r, 做一个圆柱h=r(如图1)
∵V柱-V锥
= pi*r^3- pi*r^3/3
=2/3pi*r^3
∴若猜想成立,则V柱-V锥=V半球
∵根据卡瓦列利原理,夹在两个平行平面之间的两个立体图形,被平行于这两个平面的任意平面所截,如果所得的两个截面面积相等,那么,这两个立体图形的体积相等。
∴若猜想成立,两个平面:S1(圆)=S2(环)
1.从半球高h点截一个面 根据公式可知此面积为pi*(r^2-h^2)^0.5^2=pi*(r^2-h^2)
2.从圆柱做一个与其等底等高的圆锥:V锥 根据公式可知其右侧环形的面积为pi*r^2-pi*r*h/r=pi*(r^2-h^2)
∵pi*(r^2-h^2)=pi*(r^2-h^2)
∴V柱-V锥=V半球
∵V柱-V锥=pi*r^3-pi*r^3/3=2/3pi*r^3
∴V半球=2/3pi*r^3
由V半球可推出V球=2*V半球=4/3*pi*r^3
证毕
当然,求球体体积的方法很多,较容易让人理解的是用重积分的方法
解:积分区域如图
,圆的半径为r